AES (Advanced Encryption Standard) overview Part II
In Part I of the Overview of AES (Advanced Encryption Standard) the most relevant aspects of AES and S-Box was described. Now, we discuss some details of the so-called transformations (ByteSub, ShiftRow, MixColumns and AddRoundKey) and the subkey generation process. To see more details in a more dynamic way the Rijndael Animation application is recommended.
ByteSub
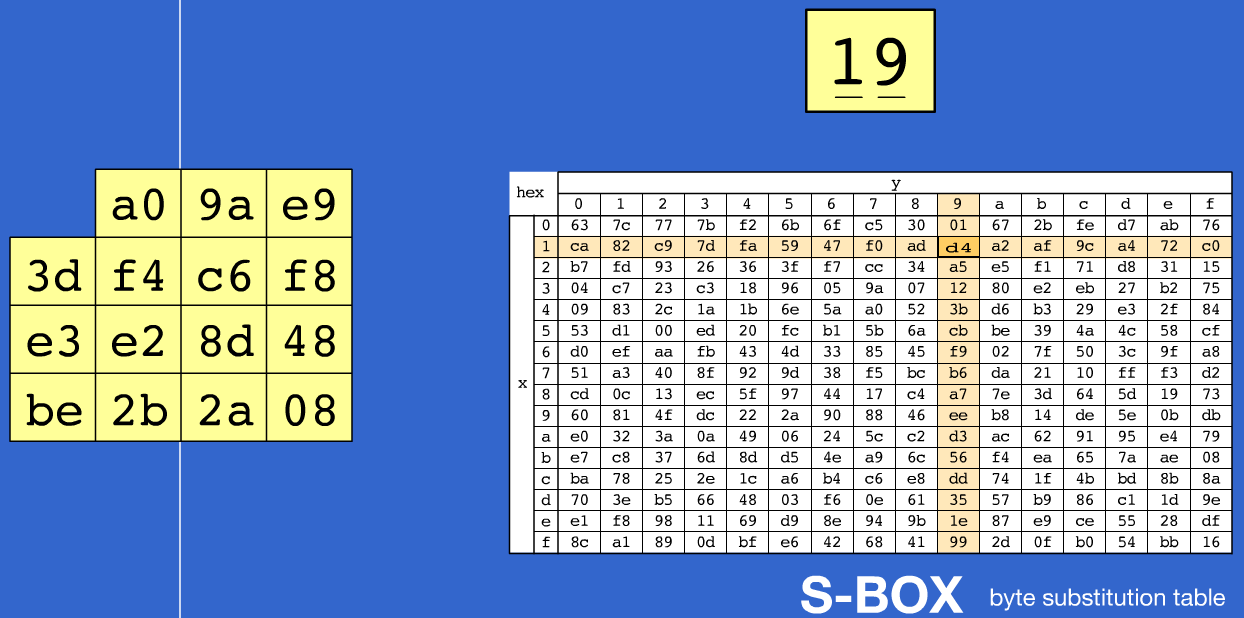
This transformation performs a byte-by-byte substitution in each of the state matrix elements, ie, the state matrix \([a_{ij}]\) is replaced by the matrix \([S_{ij}]\), Figure #1 shows this process. Using Rijndael Animation [1] application, it can be seen as the first byte of the state matrix (\([a_{00}]\)) is divided into two groups of four bits each one and they are used as pointers to the S-Box rows and columns, respectively, for replacement, in Figure #1 is shown how the value \(19\) will be replaced by \(d4\).
ShiftRow
ShiftRow applies circular left shifts, to each state matrix rows as follows: first row zero shifts, second row one shift, third row two shifts and fourth row three shifts, thus, the resultant matrix can be seen in Figure #2.

MixColumns
This transformation allows mixing the bytes of the columns, considering the bytes of each column as polynomials whose coefficients belong to \(GF(2^8)\). This function consists in multiplying the columns modulus \(x4+1\) by the polynomial \(c(x)\) where:
\[c(x)=03x^3+01x^2+01x+02\]or, in matrix form,
\[\begin{bmatrix} a'_0 \\ a'_1 \\ a'_2 \\ a'_3 \\ \end{bmatrix} = \begin{bmatrix} 02 & 03 & 01 & 01 \\ 01 & 02 & 03 & 01 \\ 01 & 01 & 02 & 03 \\ 03 & 01 & 01 & 02 \\ \end{bmatrix} \cdot \begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \\ \end{bmatrix}\]By using Rijndael Animation application [1], we can check the result of applying the above procedure, to the first column in the state matrix (see Figure #3), which is going to be replaced in the first column of the new matrix .

AddRoundKey
Let \([a_{ij}]\) be the state matrix and \([k_{ij}]\) the key matrix corresponding to that round. The AddRoundKey function, consists in performing a \(xor\) between state and key matriz (Figure #4), and then, replace it with the appropriate value.
\[AddRoundKey_{AES_{128bits}}=[a_{ij}] \oplus [k_{ij}]\]
Subkey generation
This process permits to generate sub-keys from the system key. The key is extended to a list of 4-byte words called \(W\), and containing \(N_b(N_r+1)\) words, where,
\[N_b = \frac{block \, lenth(bits)}{32}\] \[N_r = Max(N_k, N_b)+6 = Number \, of \, rounds\]The firsts \(N_k\) elements of \(W\) correspond to the key. The rest of the \(W\) elements are defined recursively, using SubByte function, cyclic shifts and \(xor\) operations. The Figure #5 shows it.

Now the RotByte function is used, which returns a word whose bytes are cyclically shifted one position to the left.
\[R_{con}[i]=(RC[i],0x00,0x00,0x00)\]being \(RC[i]\) an \(GF[2^8]\) element, defined by:
\[RC[1]=0x01, RC[i]=0x02*RC[i-1]\]Now, for \(N_k <= 6\) and for all \(i\) that is not a multiple of \(N_k\), the keywords are calculated:
\[W(i) = W(i-N_k) \oplus W(i-1)\]and for all \(i\) multiple of \(N_k\), the keywords are calculated:
\[W(i) = W(i-N_k) \oplus \begin{bmatrix} ByteSub(RotByte[W(i-1)]) \oplus R_{con} \begin{pmatrix} \frac{i}{N_k} \end{pmatrix} \end{bmatrix}\]In the case of \(N_k > 6\) the operation is the same used for \(N_k <= 6\), except when \(i\) satisfies \(i MOD(N_k=4)\) the sub-keys are calculated:
\[W(i) = W(i-N_k) \oplus ByteSub(W[i-1])\]Referencias
- http://www.formaestudio.com/rijndaelinspector/
- J A. AES - Advanced Encryption Standard. (2005) Versión 2005:
- A M. Seguridad Europea para EEUU Algoritmo criptográfico Rijndael. Madrid (2004)
- Joan Daemen VR. AES Proposal: Rijndael. NIST AES Proposal (1998)
- http://www.cryptosystem.net/aes/
- http://www.criptored.upm.es/
- http://www.kriptopolis.es/
Enjoy Reading This Article?
Here are some more articles you might like to read next: