Generalidades de AES (Advanced Encryption Standard) II Parte
En la I Parte de Generalidades de AES (Advanced Encryption Standard) se describieron los aspectos más relevantes de AES y las S-Box. Ahora, comentaremos algunos detalles de las llamadas transformaciones (ByteSub, ShiftRow, MixColumns y AddRoundKey) y el proceso de generación de subclaves. Para ver más detalles de una manera más dinámica se recomienda la aplicación Rijndael Animation.
ByteSub
Esta transformación realiza una sustitución byte por byte en cada uno de los elementos de la matriz de estado, es decir, la matriz de estado \([a_{ij}]\) se sustituye por la matriz \([S_{ij}]\), la Figura #1 muestra dicho proceso. Utilizando la aplicación Rijndael Animation de [1], se puede observar como el primer byte de la matriz de estado (\([a_{00}]\)) se divide en dos grupos de cuatro bits cada uno y se utilizan como apuntadores a filas y columnas de la S-Box, respectivamente, para realizar la sustitución, en la Figura #1 se muestra como el valor \(19\) será reemplazado por \(d4\).
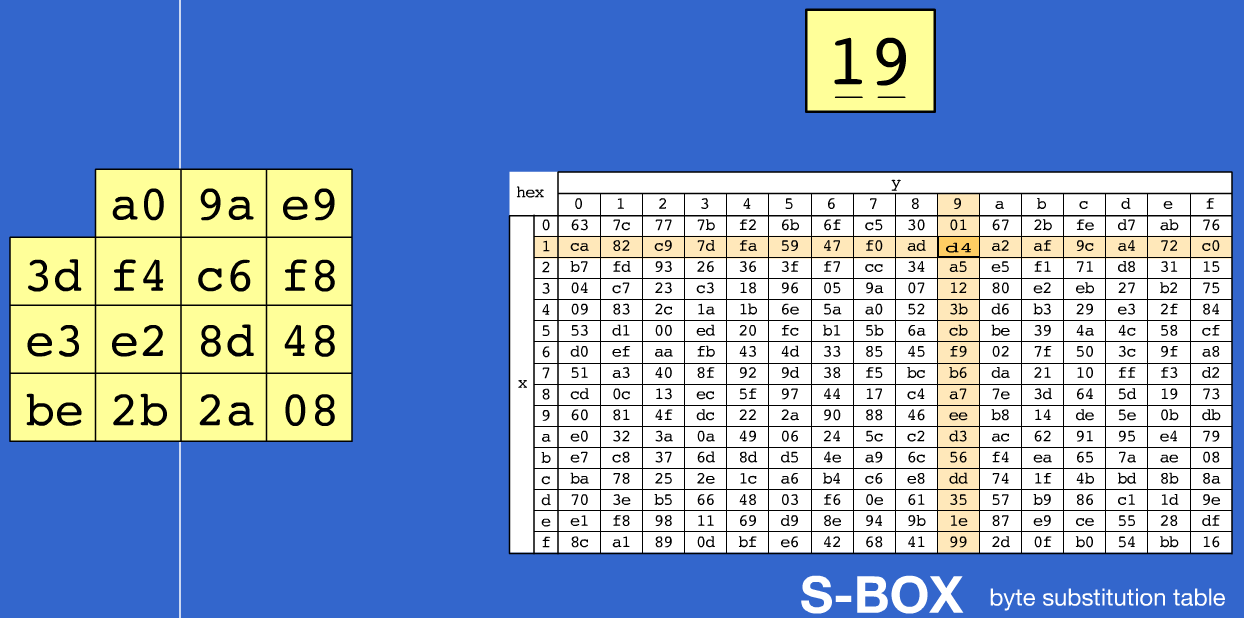
ShiftRow
ShiftRow aplica corrimientos circulares a la izquierda, a cada una de las filas de la matriz de estado de la siguiente forma: primera fila cero corrimientos, segunda fila un corrimiento, tercera fila dos corrimientos y cuarta fila tres corrimientos, de esta forma, la matriz resultante se puede apreciar en la Figura #2.

MixColumns
Esta función permite la mezcla de los bytes de las columnas, considerando los bytes de cada columna, como polinomios cuyos coeficientes pertenecen a \(GF(2^8)\). Dicha función consiste en multiplicar las columnas módulo \(x4+1\) por el polinomio \(c(x)\) donde:
\[c(x)=03x^3+01x^2+01x+02\]o, en forma de matriz,
\[\begin{bmatrix} a'_0 \\ a'_1 \\ a'_2 \\ a'_3 \\ \end{bmatrix} = \begin{bmatrix} 02 & 03 & 01 & 01 \\ 01 & 02 & 03 & 01 \\ 01 & 01 & 02 & 03 \\ 03 & 01 & 01 & 02 \\ \end{bmatrix} \cdot \begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \\ \end{bmatrix}\]Utilizando la aplicación Rijndael Animation [1], se puede comprobar el resultado de aplicar el procedimiento anterior, a la primera columna de una matriz de estado (ver Figura #3), la cual va ha ser sustituida en la primera columna de la nueva matriz.

AddRoundKey
Sea la matriz \([a_{ij}]\) la matriz de estado y \([k_{ij}]\) la matriz de la clave correspondiente a dicha ronda. La función AddRoundKey consiste en realizar una xor entre las matrices de estado y la de la clave (Figura #4), para luego, sustituir con el valor correspondiente.
\[AddRoundKey_{AES_{128bits}}=[a_{ij}] \oplus [k_{ij}]\]
Generación de subclaves
Este proceso permite generar subclaves a partir de la clave del sistema. La clave se extiende a una lista de palabras de 4 bytes que llamados \(W\) y que contiene \(N_b(N_r+1)\) palabras, donde,
\[N_b = \frac{block \, lenth(bits)}{32}\] \[N_r = Max(N_k, N_b)+6 = Number \, of \, rounds\]Los primeros \(N_k\) elementos de \(W\) corresponden a la clave. El resto de los elementos de \(W\) se definen recursivamente utilizando la función SubByte, desplazamientos cíclicos y operaciones \(xor\). En la Figura #5 se puede apreciar \(W\) en forma de arreglo.

Ahora, se utiliza la función RotByte, la cual devuelve una palabra, cuyos bytes se han desplazado cíclicamente una posición a la izquierda. Se utilizan unas constantes cuyos valores son:
\[R_{con}[i]=(RC[i],0x00,0x00,0x00)\]Siendo \(RC[i]\) un elemento de \(GF[2^8]\) definido por:
\[RC[1]=0x01, RC[i]=0x02*RC[i-1]\]Ahora bien, para \(N_k <= 6\) y para todo \(i\) que no sea múltiplo de \(N_k\), las palabras claves se calculan:
\[W(i) = W(i-N_k) \oplus W(i-1)\]y para todo \(i\) que sea múltiplo de \(N_k\), las palabras claves se calculan:
\[W(i) = W(i-N_k) \oplus \begin{bmatrix} ByteSub(RotByte[W(i-1)]) \oplus R_{con} \begin{pmatrix} \frac{i}{N_k} \end{pmatrix} \end{bmatrix}\]Para el caso de \(N_k > 6\) el funcionamiento es el mismo que para \(N_k <= 6\), excepto que cuando \(i\) satisface \(i MOD(N_k=4)\) las subclaves se calculan:
\[W(i) = W(i-N_k) \oplus ByteSub(W[i-1])\]Referencias
- http://www.formaestudio.com/rijndaelinspector/
- J A. AES - Advanced Encryption Standard. (2005) Versión 2005:
- A M. Seguridad Europea para EEUU Algoritmo criptográfico Rijndael. Madrid (2004)
- Joan Daemen VR. AES Proposal: Rijndael. NIST AES Proposal (1998)
- http://www.cryptosystem.net/aes/
- http://www.criptored.upm.es/
- http://www.kriptopolis.es/
¿Disfrutas leyendo este artículo?
Aquí hay algunos artículos más que tal vez le guste leer: